[백준 11725] 트리의 부모 찾기

 DFS 혹은 BFS 탐색을 사용하여 풀 수 있는 전형적인 문제이다.

 가중치가 없는 양방향으로 백트래킹이 필요한 트리이기 때문에

 vector<int> tree를 사용하여

출처 : 위키백과

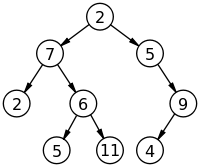
tree[2].push_back(7)

tree[7].push_back(2)...을 사용했다.

stack<int> st;                        // 지나쳐온 노드를 저장하는 stack 

vector<int> tree[100001];        // tree[i] = j (i번째 노드와 j번째 노드는 연결되어있다) 

int depth[100001];                  // 깊이를 나타낸다 (방문 여부도 검사 가능) 

int parent[100001];                // 인덱스별 부모를 저장하기 위한 배열

출처 : https://www.acmicpc.net/problem/11725

문제

루트 없는 트리가 주어진다. 이때, 트리의 루트를 1이라고 정했을 때, 각 노드의 부모를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 노드의 개수 N (2 ≤ N ≤ 100,000)이 주어진다. 둘째 줄부터 N-1개의 줄에 트리 상에서 연결된 두 정점이 주어진다.

출력

첫째 줄부터 N-1개의 줄에 각 노드의 부모 노드 번호를 2번 노드부터 순서대로 출력한다.

예제 입력 1

7
1 6
6 3
3 5
4 1
2 4
4 7

예제 출력 1

4
6
1
3
1
4

예제 입력 2

12
1 2
1 3
2 4
3 5
3 6
4 7
4 8
5 9
5 10
6 11
6 12

예제 출력 2

1
1
2
3
3
4
4
5
5
6
6

소스코드

#include<iostream> #include<vector> #include<stack> using namespace std; stack<int> st; // 지나쳐온 노드를 저장하는 stack vector<int> tree[100001]; // tree[i] = j (i번째 노드와 j번째 노드는 연결되어있다) int depth[100001]; // 깊이를 나타낸다 (방문 여부도 검사 가능) int parent[100001]; // 인덱스별 부모를 저장하기 위한 배열 int n; // DFS 탐색 void dfs(int node) { st.push(node); // root 트리 depth[node] = 0; // root 트리의 깊이는 1 parent[node] = -1; // root 트리의 부모노드는 예외처리 while (!st.empty()) { // 더 이상 방문할 곳이 없을 때까지 int next = st.top(); // 다음 node st.pop(); // 방문 for (int i = 0; i < tree[next].size(); i++) { // next와 연결되어 있는 node int next2 = tree[next][i]; // next2는 next와 연결되어 있음 if (depth[next2] == 0) { // 방문을 하지 않았다면 (깊이가 0) st.push(next2); // stack에 push depth[next2] = depth[next] + 1; // 깊이 증가 parent[next2] = next; // 부모 노드 삽입 } } } } int main() { int x, y; cin >> n; for (int i = 0; i < n-1; i++) { cin >> x >> y; tree[x].push_back(y); // 백트래킹을 해야하기 때문에 양방향으로 저장 tree[y].push_back(x); } dfs(1); for (int i = 2; i < n+1; i++) // 2번 노드부터 부모노드 출력 cout << parent[i] << '\n'; return 0; }

※ 본 글은 개인 포트폴리오 혹은 공부용으로 사용하기 때문에, 무단 복사 유포는 금지하지만, 개인 공부 용도로는 얼마든지 사용하셔도 좋습니다.